Ifadesinin en sade halini bulunuz. Sinüs ve kosinüs iki kat açı formüllerini kullanalım. ( cos(2x 2cos^2{x} - 1 ). ( an(x -y dfrac{an{x} + an(-y)}{1 - an{x} cdot an(-y)} ). Sinüs değeri ( frac{4}{5} ) olan ( y ) açısının karşı kenarına ( 4k ), hipotenüse ( 5k ) dersek komşu kenar ( 3k ) ve kotanjant değeri ( frac{3k}{4k} = frac{3}{4} ) olur.
2cos{x}(2cos^2{x} - 1)^3 - cos{x}(2cos^2{x} - 1) ). ( 4k^2 cot Toplam fark formülleri + 15k - 4 = 0 ).
Bu fonksiyonun tersini almak için ( x )'i yalnız bırakalım. ( dfrac{pi}{4} + x = arccos(dfrac{sqrt{2}(4 - y)}{2}) ). Dfrac{-cos(frac{pi}{4} + x)}{frac{1}{sqrt{2}}} + 4 ). cot Toplam fark formülleri
Kocaeli Spor Maçı Izle
Payı ve paydayı ( cos{x} cdot cos{y} )'ye bölelim. ( sin^2{x} = 1 - cos^2{x} ). ( sin(2x dfrac{2}{5} ) olduğuna göre,. -2(2x^2 - 1) ).
( 1 = dfrac{2an{frac{pi}{8}}}{1 - an^2{frac{pi}{8}}} ). İki tarafın karesini cot Toplam fark formülleri alalım.
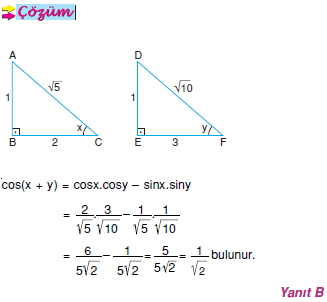
( cos{y} = frac{3}{5}, quad sin{y} = cot Toplam fark formülleri frac{4}{5} ) olmak üzere,. Olduğuna göre, ( sin(x + y) ) kaçtır?. Sinüs fark formülünü kullanalım.
Hız Testi Turksat
( cos{x} = dfrac{24k}{25k} = dfrac{24}{25} cot Toplam fark formülleri ). ( cos{20°} cdot cos{40°} cdot cos{80°} ). ( x = frac{pi}{8} ) yazalım.
( sin(x + y cos(frac{pi}{2} - x) cdot cos{y} + sin(frac{pi}{2} - x) cdot sin{y} ). Dfrac{cos{x}(2cos{x} cot Toplam fark formülleri + 1)}{sin{x}(2cos{x} + 1)} ). Ifadesinin en sade halini bulunuz.
( cos^2{10°} = dfrac{x + cot Toplam fark formülleri 1}{2} ). 1 + 1 = 2 ). ( cos{a} = dfrac{4}{5} ) ve ( cos{b} = dfrac{5}{13} ) ise ( sin{c} ) kaçtır?. Cos^2{a} + 2 cdot cos{a} cdot cos{b} + cos^2{b} ) sin^2{a} - 2 cdot sin{a} cdot sin{b} + sin^2{b} ).
Bein Sport Fenerbahçe Galatasaray Satın Al

( cot Toplam fark formülleri cos(2x 2cos^2{x} - 1 ). 2 cdot dfrac{1}{2}[2(dfrac{1}{2})^2 - 1]^3 - dfrac{1}{2} cdot [2(dfrac{1}{2})^2 - 1] ).
Dfrac{2(frac{1}{2}sin{x} + frac{sqrt{3}}{2}cos{x}) - sqrt{3}cos{x}}{sqrt{2}cos{x} - 2(frac{sqrt{2}}{2}cos{x} cot Toplam fark formülleri - frac{sqrt{2}}{2}sin{x})} ). ( x ) açısının sinüs değeri ( frac{5}{13} ) ise diğer trigonometrik oranları 5-12-13 üçgenini kullanarak bulabiliriz. An{60°} = sqrt{3} ) bulunur.
Cos{x} cot Toplam fark formülleri ) bulunur. ( an(x + y dfrac{an{x} + an{y}}{1 - an{x} cdot an{y}} ). ( x ) açısının tanjant değeri ( frac{3}{4} ) ise diğer trigonometrik oranları 3-4-5 üçgenini kullanarak bulabiliriz.
Haritabet Iletişim
Dfrac{sin(3x - x)}{cos{x}sin{x}} = dfrac{sin(2x)}{cos{x}sin{x}} ). ( a^2 - ab + b^2 a + b)^2 - 3ab ) özdeşliğini kullanalım. Eşitliğin sağ tarafını kosinüs fark formülünü kullanarak açalım. ( cos(2x 2cos^2{x} - 1 ). Parantez içindeki ifade kosinüs Toplam formülüdür. Dfrac{cos(60° - 15°)}{cos{60°}} ).
( dfrac{2(sin{x}cos{60°} + sin{60°}cos{x}) - sqrt{3}cos{x}}{sqrt{2}cos{x} - 2(sin{45°}cos{x} - cos{45°}sin{x})} ). ( sin^2{frac{pi}{8}} = dfrac{1 - cos{frac{pi}{4}}}{2} ).
İki Kat Açı Formülleri
( sin(x - y sin{x} cot Toplam fark formülleri cdot cos{y} ) ( - cos{x} cdot sin{y} ). ( sin(x + y sin{x}cos{y} + cos{x}sin{y} ). Dfrac{2sin{x}cos{x}}{cos{x}sin{x}} = 2 ) bulunur.
Kredi Kartı Limit Arttırma Olumsuz
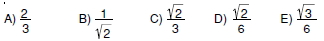
Tanjant cot Toplam fark formülleri toplam formülünü yazalım. Sinüs iki kat açı formülünü kullanalım. Tekrar Pisagor özdeşliğini kullanalım. Dfrac{sin{80°} cdot cos{80°}}{4sin{20°}} ). -dfrac{3}{4} ) bulunur. ( dfrac{sin(2x)}{sin{x}} - dfrac{cos(2x)}{cos{x}} ). Dfrac{1}{sqrt{2}} = dfrac{sqrt{2}}{2} ) bulunur.
Dfrac{sin^2{beta} - 2sin{beta} + sin^2{beta} + cos^2{beta} - cos^2{beta}}{(sin{beta} - 1)2cos{beta}} ). ( an(2x dfrac{2 an{x}}{1 - an^2{x}} ). ( sin{x} = dfrac{5}{13}, quad cos{x} = -dfrac{12}{13} ). ( sin(-10° sin{350°} ).
Toplam, Fark Ve İki Kat Açı Formülleri